[stats385] Back Propagation 이해

node by node로 본것과 matrix form으로 본것. 정리 및 스스로의 이해를 위한 부가설명.

기본적인 neural net 구조

ann-one

하나의 hidden layer가 있는 경우. 이 중 맨위의 계산에 대한 수식만을 본것. (notation 써 있는 위치)

$a_{i}$ : input layer에서 온 node ‘하나’. 그림에선 2개가 있다.

$w_{ij}$ : $a_{i}$ 에 곱해지는 weight 중 첫번째 요소. 그림에선 6개가 있으나 여기에서는 맨 위의 계산과정만을 따라가고 있다. (1x2와 2x3의 matrix)

$z_{j}$ : input layer $_{i}$ 에서 온 input에 weight을 element wise곱을 해서 합친 값에 bias $b_{j}$ 를 더한값.

$g_{j}$ : input에 weight과 bias를 계산해준 최종값( $z_{j}$ )에 씌워주는 non-linear function. ReLU나 sigmoid 등등. 이 최종 값이 새로운 input $_{j}$ 으로써 활용된다.

$w_{jk}$ : $a_{j}$ 에 곱해지는 weight 중 첫번째 요소. 그림에선 3개가 있다. (1x3와 3x1의 matrix)

따라서 ${i}$ 레이어에서 나와서 ${j}$ hidden layer를 거쳐 최종 ${k}$ layer의 output $a_{k}$ 가 나오는 과정을 식으로 나타내면 다음과 같다. back-prop1

식을 보면 알 수 있지만 당연히 최종 output $a_{k}$ 에는 $i$ 레이어에서 계산되었던 값들과 $j$ hidden layer에서 계산되었던 값들이 마치 재귀함수처럼 다 숨어 있다.

우리의 목표는 최종 output $a_{k}$ 가 우리의 target, (답이라고도 할 수 있는) $t_{k}$ 와 차이가 많이 나지 않도록 하는 것이다.

최종 target과 우리의 output의 차이, 즉 error를 계산하는 방법은 여러가지가 있는데, 가장 대표적으로 다음의 식이 쓰인다. (notation이 헷갈릴 수 있는데, ${k} \in K$ 는 최종 layer에 있는 output들을 모두 말한 것이다. 여기선 2개의 output이 있다.)

$\Large{\begin{array}{rcl} E &=& \frac{1}{2} \sum_{k \in K}(a_k - t_k)^2 \end{array}}$ loss-func

neural net을 학습시키는 것의 가장 큰 부분은 위의 error를 minimize하는 parameter의 세트 $\theta = \left\{ \boldsymbol{W} ,\mathbf{b} \right\}$ 를 찾아내는 것이다. (W,b가 bold체인것을 명심. 모든 parameter를 포함하는 notation이다)

이 문제는 nn의 핵심개념인 gradient descent를 이용하여 푸는데, 즉 $\theta$ 의 모든 parameter에 대해 $\frac{\partial E}{\partial \theta}$ 를 구하고(gradient를 구하고), $w_{jk}\leftarrow w_{jk} - \eta \frac{\partial E }{\partial w_{jk}}$ 이런 식으로 그 방향으로 parameter를 조금씩 조정(descent)해주는 것이다. ( $\eta$ 는 learning rate)

back propagation 이해

$\frac{\partial E}{\partial \theta}$ , 즉 error에 미치는 각 parameter의 영향은

$\Large{\begin{array}{rcl} E &=& \frac{1}{2} \sum_{k \in K}(a_k - t_k)^2 \end{array}}$

error의 식에 직접적으로 관여하는 $a_{k}$ 를 계산하는데 사용된 마지막 Weight (그림에선 $w_{jk}$ )
최종 output $a_{k}$ 속에 숨어 있어 좀더 간접적으로 작용하는 이전의 수많은 Weight들 (그림에선 $w_{ij}$ )가 있다.

1. output layer weights

우선 좀더 직관적인 마지막 레이어에 있는 weight의 gradient부터 살펴보자. 즉, $\frac{\partial E}{\partial W_{jk}}$ 를 계산해보자.

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{jk}} &=& \frac{1}{2} \sum_{k \in K}(a_k - t_k)^2 \ &=& (a_k - t_k)\frac{\partial}{\partial w_{jk}}(a_k - t_k) \end{array}}$

여기에서, 그리고 다음 여러 수식에는 간단한 chain rule이 쓰인다. chain rule은 간단하게 다음과 같이 나타낼 수 있다. (아시는분은 스킵)

- Chain Rule -

$\frac{\partial f(some func)}{\partial x}$ 을 구할때

$somefunc=A$ 로 치환해주고

$\frac{\partial f(some func)}{\partial x}=\frac{\partial f(A)}{\partial A}*\frac{\partial A}{\partial x}$ 의 형태로 단순화해서 구하는 것이다. (수식은 더 길어졌지만 실제 계산은 더 편하다)

예를 들어보자 $\frac{\partial f(x)}{\partial x}$ 가 아닌 $\frac{\partial f(x^2)}{\partial x}$ 를 구할때,

$\frac{\partial f(x^2))}{\partial x}=\frac{\partial f(A)}{\partial A}*\frac{\partial x^2}{\partial x}$

$=f^{‘}(A)*2$ 으로 푸는 것이다.

물론 $f(x^2)$ 를 다 전개해서 $x$ 에 대해 미분해도 되지만 somefunc이 복잡해질 수록 chain rule로 구하는게 계산이 더 수월하다.

다시 돌아와서 $\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{jk}} &=& \frac{1}{2} \sum_{k \in K}(a_k - t_k)^2 \ &=& (a_k - t_k)\frac{\partial}{\partial w_{jk}}(a_k - t_k) \end{array}}$

해당 식에서 summation기호가 사라진것은 마지막 layer의 계산에서 여러 weight가 곱해지지고 그 값을 더한거지만 $\partial w_{jk}$ 를 하면 남는 것은 $w_{jk}$ 가 관여한 식밖에 없기 때문이다. 또 $t_{k}$ 는 상수이고 $a_{k}=g(z_{k})$ 이므로

$\Large{\begin{array}{rcl}\frac{\partial E }{\partial w_{jk}} &=& (a_k - t_k)\frac{\partial}{\partial w_{jk}}a_k \ &=& (a_k - t_k)\frac{\partial}{\partial w_{jk}}g_k(z_k) \ &=& (a_k - t_k)g_k'(z_k)\frac{\partial}{\partial w_{jk}}z_k, \end{array}}$

이다. (마지막 줄에서 다시 chain rule이 쓰였다.) 이제 $\frac{\partial z_{k}}{\partial {W}_{jk}}$ 만 구하면 되는데 $z_k = b_j + \sum_j g_j(z_j)w_{jk}$ 이고 따라서 $\frac{\partial z_{k}}{\partial w_{jk}} = g_j(z_j) = a_j$ , 이므로 최종적으로 정리된 식은

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{jk}} &=& (a_k - t_k)g_k'(z_k)a_j \end{array}}$

이 중 k, 즉 마지막 레이어와 연관된 계산을 모두 $\delta_{k}$ 묶으면

$\Large{\begin{array}{rcl} \delta_k &=& (a_k - t_k)g_k'(z_k)\end{array}}$

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{jk}} = \delta_k a_j \end{array}}$

으로 최종 정리할 수 있다. 여기서 $\delta_{k}$ 는 마지막 non-linear function을 back-propagation한 것이다. 어렵당..원문( Here the $\delta_{k}$ terms can be interpreted as the network output error after being back-propagated through the output activation function, thus creating an error “signal”. Loosely speaking, Equation (5) can be interpreted as determining how much each $w_{jk}$ contributes to the error signal by weighting the error signal by the magnitude of the output activation from the previous (hidden) layer associated with each weight )

덤으로 output layer bias $b_{k}$ 는 위의 계산과정에서 $\frac{\partial}{\partial b_k} z_k = \frac{\partial}{\partial b_k} \left[ b_k + \sum_j g_j(z_j)\right] = 1$ 이므로

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial b_k} &=& (a_k - t_k)g_k'(z_k)(1) \ &=& \delta_k \end{array}}$

이다. 직관적으로 bias는 이전 layer들에서 온 값들과 관계없이 마지막에 더해지는 거니까, $k$ 번째 layer의 계산들하고만 연관이 있다는것을 확인할 수 있다.

2. Gradients for Hidden Layer Weights

앞부분은 다 똑같다.

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{ij}}&=&\frac{1}{2} \sum_{k \in K}(a_k - t_k)^2 \ &=& \sum_{k \in K} (a_k - t_k) \frac{\partial}{\partial w_{ij}}a_k \end{array}}$

summation이 여기서 사라지지 않은것에 유의! 왜냐면 이전 layer에서 온 weight는 모든 hidden layer $j$ 의 node를 계산하는데 쓰였기에 미분해도 모두 남아있다. 다시 $a_{k}=g_{k}(z_{k})$ 이므로

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{ij}}&=& \sum_{k \in K} (a_k - t_k) \frac{\partial }{\partial w_{ij}}g_k(z_k) \ &=& \sum_{k \in K} (a_k - t_k)g'_k(z_k)\frac{\partial }{\partial w_{ij}}z_k \end{array}}$

여기까진 거의 똑같은 계산과정이다. 근데 $z_{k}$ 는 $w_{jk}$ 와 직접적으로 관계를 맺고 있고 $w_{ij}$ 는 해당 식 안에서 간접적으로 관계를 맺고 있다.

$\Large{\begin{array}{rcl} z_k &=& b_k + \sum_j a_jw_{jk} \ &=& b_k + \sum_j g_j(z_j)w_{jk} \ &=& b_k + \sum_j g_j(b_i + \sum_i z_i w_{ij})w_{jk}\end{array}}$

고로 다시한번 chain rule을 써줘야 한다.

$\Large{\begin{array}{rcl} \frac{\partial z_k }{\partial w_{ij}} &=& \frac{\partial z_k}{\partial a_j}\frac{\partial a_j}{\partial w_{ij}} \ &=& \frac{\partial}{\partial a_j}a_jw_{jk}\frac{\partial a_j}{\partial w_{ij}} \ &=& w_{jk}\frac{\partial a_j}{\partial w_{ij}} \ &=& w_{jk}\frac{\partial g_j(z_j)}{\partial w_{ij}} \ &=& w_{jk}g_j'(z_j)\frac{\partial z_j}{\partial w_{ij}} \ &=& w_{jk}g_j'(z_j)\frac{\partial}{\partial w_{ij}}(b_i + \sum_i a_i w_{ij}) \ &=& w_{jk}g_j'(z_j)a_i \end{array}}$

따라서 최종값은

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{ij}}&=& \sum_{k \in K} (a_k - t_k)g'_k(z_k)w_{jk} g'_j(z_j)a_i \ &=& g'_j(z_j)a_i \sum_{k \in K} (a_k - t_k)g'_k(z_k)w_{jk} \ &=& a_i g'_j(z_j) \sum_{k \in K} \delta_k w_{jk} \end{array}}$

여기에 다시 j레이어와 관련된, 즉 j index가 들어간 모든 term을 $\delta_{j}$ 로 묶어주면

$\Large{\begin{array}{rcl} \frac{\partial E }{\partial w_{ij}}&=& a_i g'_j(z_j) \sum_{k \in K} \delta_k w_{jk} \ &=& \delta_j a_i \ \text{where} \ \delta_j &=& g'_j(z_j) \sum_{k \in K} \delta_k w_{jk} \end{array}}$

이는 결국 임의의 $l$ 번째 레이어의 weight gradient를 구하고 싶으면 error를 우리의 계산과정을 역으로 미분하고 앞에서 온 input $a_{l-1}$ 을 곱해주면 된다는것. 이부분 어렵당..원문( This suggests that in order to calculate the weight gradients at any layer $l$ in an arbitrarily-deep neural network, we simply need to calculate the backpropagated error signal that reaches that layer $\delta_{l}$ and weight it by the feed-forward signal $a_{l-1}$ feeding into that layer! )

덤으로 bias 는 이리 구해진다. 사실, 위의 식 $\delta_{j}a_{j}$ 에서 $a_{j}$ 부분만 빼주면 된다.

$\Large{\begin{array}{rcl} \frac{\partial z_k }{\partial b_i} &=& w_{jk}g_j'(z_j)\frac{\partial z_j}{\partial b_i} \ &=& w_{jk}g_j'(z_j)\frac{\partial}{\partial b_i}(b_i + \sum_i a_i w_{ij}) \ &=& w_{jk}g_j'(z_j)(1), \ \text{giving} \ \frac{\partial E }{\partial b_i}&=& g'_j(z_j) \sum_{k \in K} \delta_k w_{jk} \ &=& \delta_j \end{array}}$

Matrix Form Backpropagation 이해하기

역시 차원이 많아지면 matrix가 보기에 짱.

$Input=x$ , $Output=f(Wx+b)$ 은 여전히 유효하다. 아니, 여기서는 bias가 없다. (실제로 빈번히 이렇게 쓰는듯)

Neural Network

식으로 정리하면 (볼드체 안썻지만 모두 상수가 아니다)

Input=

$x_{0}$ Hidden Layer1 output

$=x_{1}=f_{1}(W_{1}x_{0})$ Hidden Layer2 output

$=x-{2}=f_{2}(W_{2}x_{1})$ Output

$=x_{3}=f_{3}(W_{3}x_{2})$

여기에서도 다음과 같은 식으로 error를 계산한다

$E=\frac{1}{2}\left|x_{3}-t\right|_{2}^2$ 여기서 subletter2는 유클리드 놈을 의미한다.

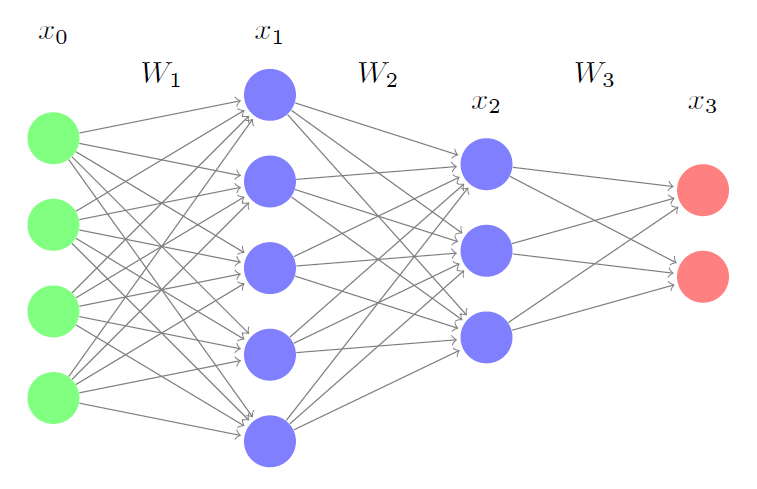
input $x_{0}$ 을 넣어서 output $x_{3}$ 이 나왔고, 이를 토대로 $W_{1},W_{2},W_{3}$ 를 바꿀 것이다. 역시나 같은 방식으로,

$w=w−α_{w}\frac{∂E}{∂w}$ for all the weights $w$ 이렇게 구한다.

이제 $W_{3}$ , 즉 마지막 weight의 gradient 부터 구해보자. 참고로 앞의 그림에서 $W_{3}$ 의 크기는 (2x3), $x_{2}$ 의 크기는 (3x1)였다.

$E=\frac{1}{2}\left|x_{3}-t\right|_{2}^2$ (다시 상기)

matix1

첫줄에서 $t$ 는 상수이므로 편미분에서 사라지고, 다시 chain rule을 사용해서 결국 이전 layer의 값인 $x_{2}^{T}$ 만이 남았다. (위 식에서 전치 $T$ 는 matrix 연산의 특징이라 이해하면 된다. 사실 손으로 다 해보면 전치가 붙어야됨을 볼 수 있다. 자세한 내용은 Matrix Calculus참고. 추가 Transpose를 손으로) 이는 앞에서 node by node로 보았을때와 거의 유사하다.

여기서 ∘는 Hadamard product라고 단순 내적형태의 행렬곱이 아니라 같은 위치에 있는 원소끼리의 곱을 의미한다.

다음으로 $W_{2}$ 에 대해 보자.

matix2

세번째 줄까진 $W_{3}$ 와 똑같으나 $W_{3}x_{2}$ 가 $W_{2}$ 로 바로 미분이 안되고 안에 내재되어 있던 계산까지 들어가 미분을 하였다. (node by node에선 여기서 summation기호가 있었으나, 여기선 어차피 matix, 즉 전체를 포함하는 개념이라 summation이 안쓰였다.)

이제 슬슬 힘듬….이제 마지막 $W_{1}$ 에 대해 보면 matix3

ㅋㅋ수식이 많이 불친절해졌다. 그러나 $W_{2}$ 를 계산할때와 마찬가지로 마지막 미분에서 한번더 쪼개서 계산을 하였다는 것은 완전히 동일하다.

정리

위의 계산들을 정리해보자면, $L$ 개의 layer가 있고 그에 따라 L개의 Weight $W_{1},..,W_{L}$ 과 각각의 non-linear function이 있으면,

Forward Pass(원 방향 계산)는

$x_{i}=f_{i}(W_{i}x_{i-1})$

이렇게 이루어 지고, Error는 다음과 같이 계산된다.

$E=\frac{1}{2}\left\|x_{L}-t\right\|_{2}^2$

Backward Pass에서는 마지막 layer의 backprop과 그 이전 layer들의 backprop으로 나뉘는데, 요렇다. matix4

위에서 정의한 $\delta$ 들을가지고 요렇게 weight 를 update를 할 수 있다.

matix5

참조: 행렬미분 : https://datascienceschool.net/view-notebook/8595892721714eb68be24727b5323778/

행렬 back prop: https://sudeepraja.github.io/Neural/

node back prop: https://theclevermachine.wordpress.com/2014/09/06/derivation-error-backpropagation-gradient-descent-for-neural-networks/

Deep Learning Math

기본적인 neural net 구조

back propagation 이해

1. output layer weights

2. Gradients for Hidden Layer Weights

Matrix Form Backpropagation 이해하기

정리

Comments

Related Posts

[Code implementation] Bayesian Gaussian mixture 22 Oct 2019

[Code implementation] Gaussian mixture 15 Oct 2019

[데이터분석 정리]HDBSCAN 이해하기 (with python) 15 Jul 2019